How to tile multiple trapezoids in a rectangle?

[ChrisCAD]

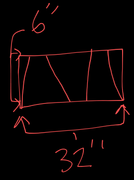
The goal is a perfectly continuous fill, where the trapezoids align edge to edge and fully occupy the rectangular boundary with no gaps or overlaps inside a rectangle of fixed length and height. I have a 32"x6" piece of sheet metal bar that I need to draw 3 trapezoids the exact same size from corner to corner of the metal sheet. How do I do this?

[CVH]

Hi,

There are some constrains missing to complete the answer.

First: You probably refer to isosceles trapezoids (trapeziums) ...
... Otherwise you must at least specify some details about the trapezoids.

Then for 3 identical isosceles trapezoids:
As on your draft the bottom edge of 32" long is equal to: 2x the longer edge (base A) and 1x the shorter edge (base B).
The top 32" edge is equal to: 1x the longer edge, 2x the shorter edge and 2 remaining parts.
The remaining parts are triangles and the edge (C) of interest is (base A - base B)/2 long.

Meaning that:
Bottom 32" = 2x A + 1x B
Top 32" = 1x A + 2x B + 2x (A - B)/2 and simplified that is also equal to 2x A + 1x B

Any combination that fits the 2x A + 1x B = 32" relation is a solution.
For example: 13" and 6" or 12" and 8" or 15" and 2" ... And so on (10" 2/3 < A < 16")

You need to specify an extra constrain.
For example: B = A / 2
Then the result becomes fixed: 32" = 2.5x A => A = 12.8", B = 6.4"
What remains (C) is (12.8 - 6.4)/2 long or 3.2" at both sides.
The acute angles of this isosceles trapezoid are 61.927513.. degrees = atan(6.0 / 3.2)

Another constrain could be: Acute angle = 45 degrees. (36.869898.. < angle < 90)
Then B = A minus 2 times 6". (tan(45) = 1.0 => C = 6.0")
=> 32" = 2x A + (A - 12") or A = 14.666...", B = 2.666..."

It is a bit more complicated when you specify the isosceles trapezoids equal legs length. (e.g this topic)
For example 7.5" long legs. (6" < leg < 10")
Then C is sqrt(7.5² - 6²) long = 4.5"
A is then equal to B + 9"
=> 32" = 3x B + 18" or B = 4.666...", A = 13.666..."
The acute angles of this isosceles trapezoid are 53.130102.. degrees = acos(4.5 / 7.5)

The Math can be expanded to more than 3 identical isosceles trapezoids.
And further expanded for: Acute, Right, Obtuse or 3 equal sided trapezoids.

Note that this doesn't account for 2 parallel offsets for the cutting width.
Including that is much more complicated.

Regards,
CVH

[ChrisCAD]

Thank you. I figured it out.